- Рандомыч, глянь гитару.
- Симпатичная. А что с ней?
- То ли не строит, хотя и строит, то ли у меня что с головой.
- Как проверяешь настройку?
- Ну, как обычно, по флажолетам.
- Да… Знаешь, в средние века ходила такая байка: «если лютнист живет шестьдесят лет, то двадцать из них он настраивает свой инструмент».
- Ха! Точно. Но почему так всегда?
- Гитару настроить чисто и правильно одновременно невозможно.
- Как это? Почему это? И как понимать эти четыре наречия подряд?
- Хорошо. У нас с тобой нет музыкального образования, и как дилетант дилетанту я тебе расскажу. Флажолеты как звучат? На каких частотах?
- Ну… на кратных, видимо… обертоны…
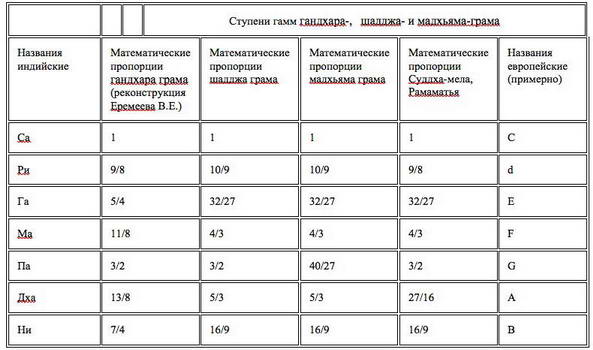
- Верно. Интервалы частот, выраженные простыми дробями, называют с древности чистыми. По длине струны ½ - октава, 2/3 - квинта, ¾ — кварта. И музыкальный строй древних индусов, китайцев, греков опирался на эти интервалы. Например, смотрим в книжке Алексея Насретдинова индийские звукоряды
и сравнение древних греческого и китайского:
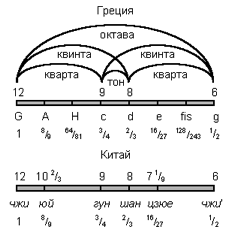
Пифагор на своем монохорде подобрал интервалы для нот внутри октавы, выраженные простыми дробями, и люди пользовались этим строем две тысячи лет. Но проблемы с подобными ладами всегда заключались в невозможности сыграть мелодию чуть выше или чуть ниже, так как при сдвиге на ступень изменяются интервалы между соседними нотами мелодии, т.е. по сути получается другая мелодия. А на древних лютнях не было фиксированных ладов, лады образовывались жильными перевязями на грифе, которые можно было перемещать вдоль грифа. Потому процесс настройки был крайне серьезным мероприятием. Соответственно, и с полифонией проблемы, в аккордах диссонансы, биения и всякая такая вещь. Давай посмотрим на древний европейский звукоряд, в котором частоты звуков имеют соотношение 4:5:6
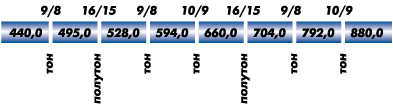
и обратим внимание на интервалы между соседними звуками:
Конечно же, это не тон и полутон в современном понимании. Но главное – тон 9/8 не равен тону 10/9 и ни один из них не равен двум полутонам 16/15, т.е. шкала неравномерная.
Этой проблемой в средние века занимались и китайцы, и европейцы. Как выровнять строй?
И вот в 1584-1596 Чжу Цзай-юй (1536-1610), ученый, астроном, математик, лингвист и музыковед разработал и предложил новую теорию музыкального строя. Именно он предложил при расчете длин струн, соответствующих ступеням звукоряда, использовать геометрическую прогрессию со знаменателем 12√2. Т.е. октава разбивалась на 12 полутонов, и соотношение частот звуков с интервалом в полутон было равным 12√2. Это был поистине настоящий прорыв в поиске темперированного, т.е. выровненного строя. Исследователи Кобзев А.И., Еремеев В.Е. отмечают: «Однако столь выдающееся изобретение не было воспринято в Китае. Лишь через полтора с лишним века о нем адекватно отозвался Цзян Юн 江永 (1681-1762), всю жизнь занимавшийся математикой и музыкой, но только на восьмом десятке сумевший познакомиться с «Люй ли цюань шу». Понадобилось еще более чем полтора столетия и смена культурной парадигмы, чтобы в 1933 Лю Фу впервые дал ему точную научную оценку. Напротив, на Западе это достижение ожидал триумф. На рубеже XVI-XVII вв. начали налаживаться систематические контакты Китая с Европой, куда, видимо, достаточно быстро проникла идея равномерной темперации. Первое упоминание о ней появилось в неопубликованных бумагах великого нидерландского ученого и инженера Симона Стевина (1548–1620), а ее публикация состоялась в 1636 во «Всеобщей гармонии» («Harmonie Universelle») французского монаха-минорита, теолога, физика и музыкального теоретика Марена Мерсенна (1588–1648). К концу XVII в. темперированный строй исследовал немецкий музыкальный теоретик и акустик Андреас Веркмейстер (1645–1706), которому часто приписывается его изобретение, а в 1722 увидел свет эпохальный «Хорошо темперированный клавир» («Das Wohl-temperierte Klavier») И.-С. Баха, представивший первые музыкальные произведения (прелюдии и фуги) в темперированном строе и положивший начало его распространению в мире.»
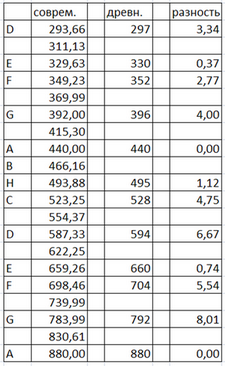
Сравним теперь частоты небольшого диапазона древнеевропейского строя и современного темперированного:
В правой колонке зафиксированы разности частот соответствующих ступеней звукоряда. Такие микроинтервалы в теории музыки называют коммами. Измеряют их в долях тона или в центах. Если отношение частот интервала обозначить как q, то количество центов в данном интервале определяется формулой С=log2q*1200. Видно, что ста центам соответствует полутон.
Но вернемся к гитаре. Лады расположены таким образом, что длина звучащей части струны, зажатой на любом из ладов, принадлежит той самой геометрической прогрессии со знаменателем 12√2. Т.е. эти длины выражаются иррациональными числами, и, как видно в таблице, за исключением октав, все остальные интервалы отличны от чистых, выражаемых простыми дробями. Итак, проверить флажолетами, т.е. чистыми интервалами, строй гитары теоретически невозможно. Практически же, разности интервалов достаточно малы, и уловить их на слух, могут далеко не все. В мелодии, когда звуки идут последовательно, эти микроотступления темперированного строя от чистого не столь заметны, но стоит взять аккорд, как ты слышишь какие-то напряжения, биения. Подстрой, к примеру, струны так, чтобы какое-то обращение аккорда звучало ясно и чисто, и возьми другое обращение того же аккорда! Сразу убедишься, что звучит оно не так чисто, т.к. интервалы созвучий перераспределяются между струнами, и внесенные микропогрешности удваиваются.
- Так что же это получается… В угоду равномерности утрачена чистота?
- Так точно.
- Вот так фокус. Печально.
- А иначе что получится? Каждый раз при переходе из одной тональности в другую – перестраивать фортепиано или, скажем, орган.
- Да уж.
- Потому, воспроизвести музыку древних можно далеко не на всех современных инструментах.
- Понятно… только на тех, где можно плавно менять частоту звука… скрипка, кулисный тромбон…
- Да. Так что с гитарой проблема практически та же, что и у средневековых лютнистов. Даже если конструктивно гитара изготовлена идеально, вечно будешь настраивать и подстраивать. Кстати, предлагались и существуют темперированные строи с октавой из другого числа равных интервалов, например, 24 или 53. В них микроотклонения от чистых интервалов, понятно, меньшие, и всё же они есть.



Интересно, а с какой целью на гитаре логарифмы в бантики завязаны?!
Бантики как раз иллюстрируют произвольность положения ладов на древней лютне и возможность, передвигая лады, менять интервалы между ступенями октавы. Что касается логарифмов, то Чжу Цзай-юю пришлось обойтись в своих расчетах без них, поскольку логарифмы были изобретены Джоном Непером около 1594 года, а его первая работа об этом «Описание удивительной таблицы логарифмов» была опубликована лишь в 1614 году. Но ко времени создания первого фортепиано (1700 г.) логарифмы уже прочно вошли в обиход ученых и могли облегчить труд продвинутых мастеров — изготовителей музыкальных инструментов.
Очень интересно!:)
Отлично, спасибо! Давно интересовался историей современных разбиений на ноты и октавы.
Остался (для меня) открытым вопрос, почему для оркестра для каждого инструмента все партии повышают или понижают?
Вопрос требует отдельного изучения. Может из профессиональных музыкантов кто подскажет.